排序算法
复杂度
老是听别人说O(N),O(logN),O(N²),我们也装着样子喊着,那到底什么是时间复杂度呢?什么是空间复杂度呢?怎么算出来的呢?为什么这个算法是O(N),另一个又是O(logN),为什么需要复杂度呢?
为什么需要复杂度
- 测试结果非常依赖测试环境
测试环境中硬件的不同会对测试结果有很大的影响。比如,我们拿同样一段代码,分别用Intel Core i9处理器和Intel Core i3处理器来运行,不用说,i9处理器要比i3处理器执行的速度快很多。还有,比如原本在这台机器上a代码执行的速度比b代码要快,等我们换到另一台机器上时,可能会有截然相反的结果。
- 测试结果受数据规模的影响很大
后面我们会讲排序算法,我们先拿它举个例子。对同一个排序算法,待排序数据的有序度不一样,排序的执行时间就会有很大的差别。极端情况下,如果数据已经是有序的,那排序算法不需要做任何操作,执行时间就会非常短。除此之外,如果测试数据规模太小,测试结果可能无法真实地反应算法的性能。比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快!
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。
那怎么算出这些复杂度呢
const fn = (n)=>{
let sum = 0;
let i = 0
for(;i<n;i++){
sum = sum + i
}
return sum
}
在考虑时间复杂度时,我们站在CPU的角度进行观察,CPU在运算每行代码时,无非是进行 读数据 - 处理数据 - 写数据 三个环节,我们初定这三个环节需要花费1个单位时间 unit-Time
以上诉代码为例
第2,3,6行代码执行了1次,而三四行代码需要执行n次,这里的n指的就是传入函数的参数数据量
那么整个函数跑下来需要花费 n+3 * unit-Time的时间,而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了
所以使用大O表示法的时候值记录最大量级O(n)
那空间复杂度呢
一个道理,时间复杂度是以时间为维度,那空间复杂度就是以函数里创建了多少空间为维度去进行计算。
常见排序算法的时间复杂度和空间复杂度
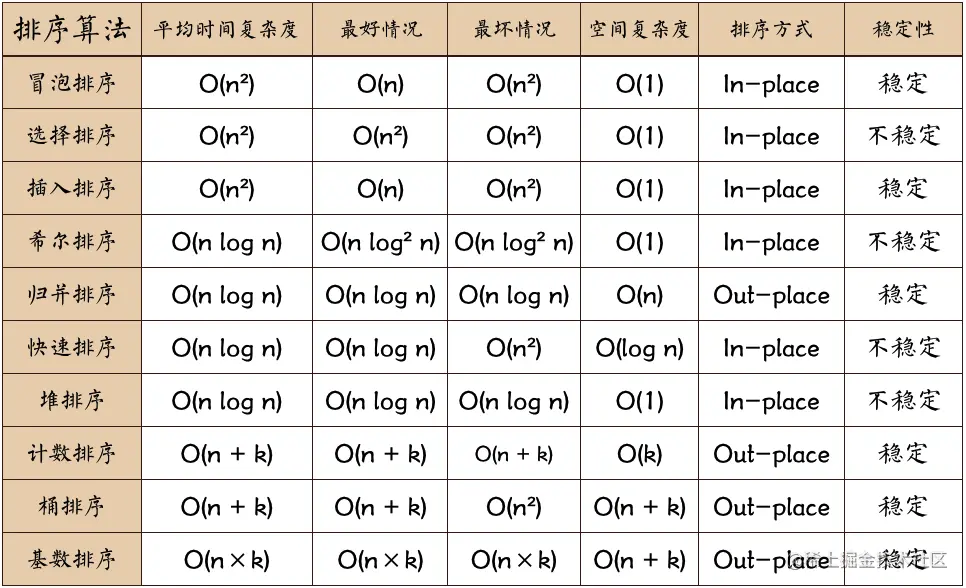
术语解释:
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面,反之为不稳定
- In-place:是否在源数据上进行排序
- k:桶的个数
冒泡排序
这个大家都知道的,直接上代码
const bubbleSort = (arr)=>{
let len = arr.length;
for (let i = 0; i < len; i++) {
for (let j = 0; j < len - 1 - i; j++) {
if(arr[j]>arr[j+1]){
[arr[j],arr[j+1]] = [arr[j+1],arr[j]]
}
}
}
}
可以明显看出来,是做了循环的遍历嵌套,而时间复杂度是O(n²),空间复杂度是创建的i和j,是常量级别的,所以空间复杂度是O(1)
选择排序
选择排序的思路是:寻找后续列表中最小(最大)的与列表最前面的未被排序过的进行交换
const selectSort = (arr)=>{
let len = arr.length
for (let i = 0; i < len; i++) {
//从头按顺序选择幸运观众(凑合选着先)
let minIdx = i
//遍历i以后的列表,找一个小于或者大于幸运观众的值,选他为幸运观众(选幸运观众)
for (let j = i+1; j < len; j++) {
if(arr[j]<arr[minIdx]){
minIdx = j
}
}
//交换位置,给幸运观众排座位
[arr[i],arr[minIdx]] = [arr[minIdx],arr[i]]
}
}
时间复杂度就是 O(n²),空间复杂度也还是常量级别的O(1)
插入排序
插入排序的思路是:选择一个key值,去跟key左侧(已排序的区域进行比较,已排序的区域的值大于(小于)key的右移),直到已排序的值小于(大于)key,则就当前位置复制key,做插入操作
普通版
const insertSort = (arr)=>{
let len = arr.length
for (let i = 1; i < len; i++) {
//获取一个基准值
let key = arr[i]
//复制基准值的位置
let j = i - 1
//寻找小于基准值的值
while (j>=0 && arr[j] > key) {
//不符合条件的都一边去,靠边站
arr[j+1] = arr[j]
j--
}
//在对应位置将基准值插入
arr[j+1] = key
}
}
时间复杂度就是 O(n²),空间复杂度也还是常量级别的O(1)
二分查找
由于左侧已排列好的是一个单调的区域,所以可以考虑用二分查找去查找插入的位置,减少复杂度
const binaryInsertionSort = (arr)=>{
let len = arr.length
for(let i = 0;i<len;i++){
//获取基准值
let key = arr[i]
//寻找基准值位置,二分查找
let l = 0,r = i - 1
while(l<=r){
let mid = l + ((r-l)>>1)
if(arr[mid]>key){
//如果中值大于基准值,说明基准值应该插在中值的左侧
r = mid - 1
}else{
//如果中值小于基准值,说明基准值应该插在中值的右侧
l = mid + 1
}
}
for (let j = i - 1; j >= l; j--) {
arr[j + 1] = arr[j];
}
arr[l] = key;
}
}
希尔排序(做预处理的插入排序)
希尔排序的思路是:作为插入排序的优化,又称减少增量排序
使用插入排序,通过比较相距一定间隔(增量)的元素,每次比较所用的距离随着算法的进行而缩小,直到比较到相邻元素为止。
const shellSort = (arr)=>{
let len = arr.length
//控制比较间隔
for(let gap = len >> 1; gap>0 ; gap = gap >> 1 ){
for (let r = gap; r < len; r++) {
//同插入排序的步骤:
//选择基准值
//复制基准值位置
let j = r
let key = arr[r]
//比较
if(arr[j] < arr[j - gap]){
while (j - gap >= 0 && key < arr[j - gap]) {
arr[j] = arr[j - gap]
j -= gap;
}
//插入
arr[j] = key
}
}
}
}
T(n)= 2T(n/2)+c
= 4T(n/4)+2c
……
= 2^kT(n/(2^k)) + kc
时间复杂度是:O(nlogN),空间复杂度是常量级的O(1),不稳定
归并排序
归并的思路是使用了分治法,将整体拆成局部,通过局部的排列去扩散到全局排序
const mergeSort = (arr)=>{
if(arr.length<2) return arr
//将传入的数组二分开,一直到只剩一个
const mid = arr.length >> 1
let left = arr.slice(0,mid)
let right = arr.slice(mid)
const merge = (left,right) =>{
const tempArr = []
while (left.length && right.length) {
//可以想象成两个队伍,从矮到高排列成一条队伍
if(left[0]<right[0]){
tempArr.push(left.shift())
}else{
tempArr.push(right.shift())
}
}
return [...tempArr,...left,...right]
}
//两个部分拆到最小
left = mergeSort(left)
right = mergeSort(right)
return merge(left,right)
}
在运算中,mergeSort用公式法计算时间复杂度
T(n) = 2T(n/2) + c
= 4T(n/4) +2c
……
= 2^kT(n/(2^k)) + kc
= 2^kT(1) + nc
……
=2^k = n
k = log2为底的N次幂
//大O表示法,除开常量
=log2为底的N次幂 * T(1)
所以时间复杂度是O(logN)
在运算中,merge的时间复杂度是N
所以归并的时间复杂度是O(nlogn),空间复杂度是tempArr的长度,也就是arr的长度,故为O(n),并且归并算法并不是在源数据上进行处理,所以是Out-place的
快速排序
快排的思路就是:选择一个基准值,比基准值小的放基准值的左边,比基准值大的放基准值的右边,然后再递归基准值两侧的数组
普通版
const quickSort = (arr,left,right)=>{
if(arr.length<2) return arr
let len = arr.length
let lessArr = []
let moreArr = []
//随机选
let pivot = Math.floor(Math.random()*len)
let key = arr[pivot]
for (let i = 0; i < len; i++) {
if(arr[i]<key && i !== pivot){
lessArr.push(arr[i])
}
if(arr[i]>key && i !== pivot){
moreArr.push(arr[i])
}
}
return [...quickSort(lessArr),arr[pivot],...quickSort(moreArr)]
}
这个方法虽然也可以进行快排,并且也符合快排的思路,但是并不是原地排序,还浪费了不少空间复杂度
三路快排
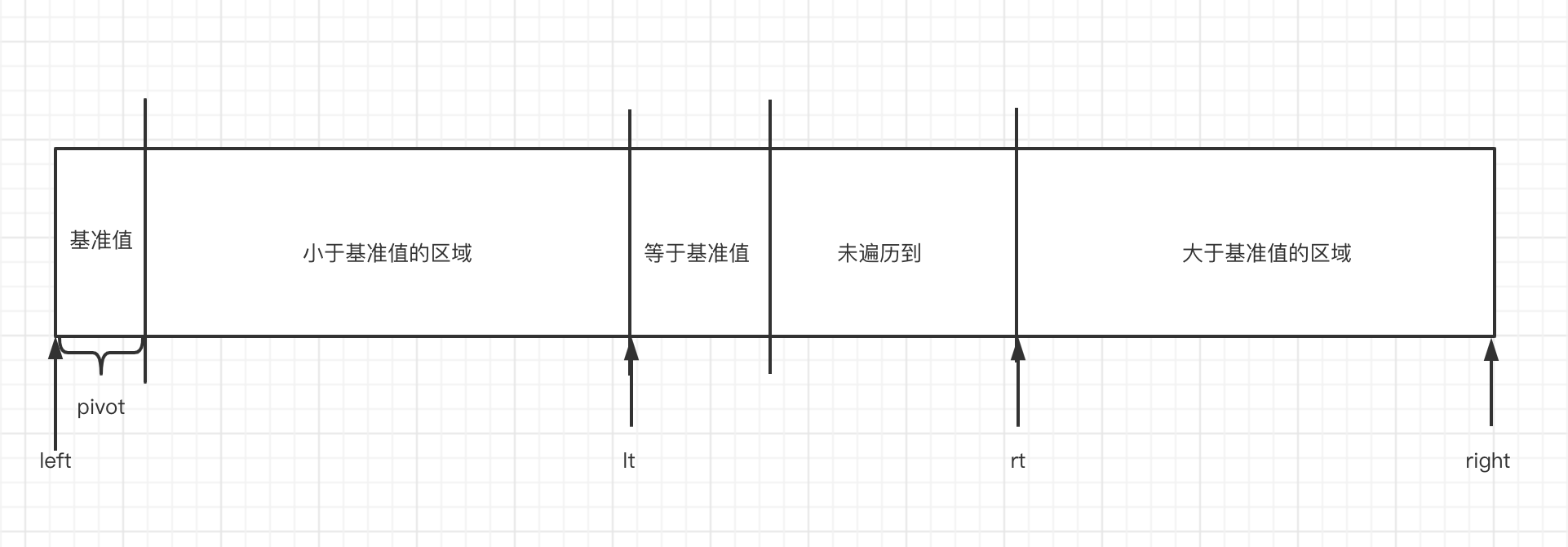
思路:
在源数据中划分三个区域:小于基准值,大于基准值,未遍历到的区域
从一开始选择最左为基准值,遍历数组
三个规则:
- 等于基准值的,i++,不做处理,继续遍历
- 小于基准值的,lt记录的是小于基准值区域末位idx,arr[lt]与当前遍历值交换,i++,lt++(扩大小于基准值的区域)
- 大于基准值的,rt记录的是大于基准值区域的头部idx,arr[rt]与当前遍历值交换,rt- -(缩小基准值的区域)
const threePathQuickSort = (arr,left,right)=>{
if(left >= right){
return false;
}
const areaObj = pieceArea(arr,left,right)
threePathQuickSort(arr,left,areaObj.left)
threePathQuickSort(arr,areaObj.right,right)
}
const pieceArea = (arr,left,right)=>{
let pivot = arr[left]
//左区间(小于基准值区域 默认为空)
let lt = left
//右区间(大于基准值区域 默认为空)
let rt = right + 1
for (let i = left + 1; i < rt;) {
if(arr[i] === pivot){
i++
}else if(arr[i] > pivot){
//大于基准值,将当前值归到rt区间里
[arr[rt - 1],arr[i]] = [arr[i],arr[rt - 1]]
rt--
}else{
//小于基准值,将当前值归到lt区间中
[arr[lt + 1],arr[i]] = [arr[i],arr[lt + 1]]
lt++
i++
}
}
//将基准值跟左区间交换
[arr[left],arr[lt]] = [arr[lt],arr[left]]
lt--
console.log(`三路快排后的数组: ${arr}`);
return {left:lt,right:rt}
}