位操作符 | ZJX's Blog

前情提要

由于JavaScript不是强类型语言。与许多其他编程语言不同，JavaScript不定义不同类型的数字，我们只有number(BigNum)用来定义数字，而不需要像其他强类型语言一样需要定义特定的数据类型比如整数int、浮点数（double，float…）等等。

位运算直接对二进制位进行计算，位运算直接处理每一个比特位，是非常底层的运算，好处是速度极快，缺点是很不直观，并且在JS中…位运算很吊诡，许多场合不便于使用（下面会提到），还是不建议使用嗷。

诡异情况

情况1

let a = 2e9 // 2 * 10^9   2000000000
parseInt(2e9).toString(2) // '1110111001101011001010000000000'
console.log(parseInt(2e9).toString(2).length) //31
a<<1   //-294967296
//原本只是想做个骚一点的a * 2的操作，这结果是什么鬼！

情况2

//将16进制的 100000000 转成十进制
let a = parseInt('100000000',16) //4294967296 
parseInt(4294967296).toString(2)// '100000000000000000000000000000000'
console.log(parseInt(4294967296).toString(2).length) //33

//将2进制的 1111 转成十进制
let b = parseInt('1111',2) // 15

a | b //15 
//这！！！这a怎么变假值（0）了！

这就能解释上面的吊诡现象了…如果不能确定被操作数的位数，还是不建议使用位运算符……

但是还是得了解一下的嘛，那么骚的东西（狗头）

学习时间到

~~给我O泡给我O泡~~

以下例子以64位做例子演示

1、按位与（AND）`&`

&，用大学时期记法就是一假则假

以特定的方式组合操作二进制数中对应的位的值，如果对应的位的值都是1，结果才为1，如果任意一位为0则结果就是0

比如5 & 8，因为是位运算，所以会隐形得转成二进制
parseInt(5).toString(2) //十进制转二进制
//'101'
在进行位运算时，高位补0
//5的二进制表示为: 00000000 00000000 00000000 00000101
//8的二进制表示为: 00000000 00000000 00000000 00001000
-----------------------------------------------------
按位做与操作，答案为00000000 00000000 00000000 00000000
返回的值会转回十进制
console.log(5 & 8) //0

2、按位或（OR）`|`

|，用大学时期记法就是一真则真

|运算符跟&的区别是，如果对应的位的值任意一位为1，则结果就是1，如果对应的位的值都是0，结果才为0

比如5 | 8，因为是位运算，所以会隐形得转成二进制
parseInt(5).toString(2) //十进制转二进制
//'101'
在进行位运算时，高位补0
//5的二进制表示为: 00000000 00000000 00000000 00000101
//8的二进制表示为: 00000000 00000000 00000000 00001000
-----------------------------------------------------
按位做或运算，答案为00000000 00000000 00000000 00001101
返回的值会转回十进制
console.log(5 | 8) //13

3、按位异或（XOR） `^`

^，用大学时期的记法就是一真才真

^如果对应的位的值，有且只有一位为1时，结果为1，其余都是0

比如5 ^ 9，因为是位运算，所以会隐形得转成二进制
parseInt(5).toString(2) //十进制转二进制
//'101'
在进行位运算时，高位补0
//5的二进制表示为: 00000000 00000000 00000000 00000101
//9的二进制表示为: 00000000 00000000 00000000 00001001
-----------------------------------------------------
按位做或运算，答案为00000000 00000000 00000000 00001100
返回的值会转回十进制
console.log(5 ^ 9) //12

4、按位非（NOT）`~`

~，同字面意思，对应每位取反（包含符号位），也就是求操作数的反码

便捷记法：结果为操作数取反 - 1

比如~ 3，因为是位运算，所以会隐形得转成二进制
parseInt(3).toString(2) //十进制转二进制
//'1'
在进行位运算时，高位补0
//1的二进制表示为: 00000000 00000000 00000000 00000011
//按位取反-------------------------------------------
//11111111 11111111 11111111 11111100 
你以为就这样输出了？你以为答案是这么大的数？
你只在第二层
大气层在这↓↓↓↓↓
由于第一位符号位为1，故其为负数，展示则为该结果的补码
//原码：11111111 11111111 11111111 11111100
//补码 === 反码（除了符号位外，按位取反） + 1
//补码：10000000 00000000 00000000 00000100
再在补码的十进制前补上负号则得出结果
console.log(~3) //-4

5、左移`<<`

<<运算符使目前操作数的二进制所有位（包括符号位）都左移制定位数，抛弃高位，低位补0

便捷运算：左移多少位，也就是乘以 2的几次方

比如3<<2，因为是位运算，所以会隐形得转成二进制
parseInt(3).toString(2) //十进制转二进制
//'11'
在进行位运算时，高位补0
//3的二进制表示为: 00000000 00000000 00000000 00000011
3 << 2,所有位左移两位,舍弃高位，保证32位，低位补0
-----------------------------------------------------
左移运算，答案为00000000 00000000 00000000 00001100
console.log(3 << 2) //12

6、右移`>>`

聪明，没错，跟你想的一样，那我就不细嗦了

才怪

右移有一点要注意的，右移之后，被移出位被丢弃，左边少的位数是用最左侧的位拷贝填充

比如8>>2，因为是位运算，所以会隐形得转成二进制
parseInt(8).toString(2) //十进制转二进制
//'1000'
在进行位运算时，高位补0
//3的二进制表示为: 00000000 00000000 00000000 00001000
8 >> 2,所有位右移两位,丢弃移出的位，保证32位，高位用操作数最左边位的值复制填充
-----------------------------------------------------
左移运算，答案为00000000 00000000 00000000 00000010
console.log(8 >> 2) //2

比如-8>>2,因为是位运算，所以会隐形得转成二进制
parseInt(-8).toString(2) //十进制转二进制
//'-1000'
个屁咧，用补码记录负数！！！！！！
先是抛弃符号位的源码：00000000 00000000 00000000 00001000
然后取补码：11111111 11111111 11111111 11111000
-8 >> 2再右移两位
-------------------------------------------------------
结果就是：11111111 11111111 11111111 11111110
转回展示的十进制，再补一次
补码：00000000 00000000 00000000 00000010
再在补码的十进制前补上负号则得出结果
console.log(-8 >> 2) //-2

7、无符号右移 >>>

同上述右移，只不过高位都是用0填充

位运算符的妙用

1.用按位与判断奇偶数

通过和1进行与运算，利用一假则假的特性，判断二进制最低位的值，从而判断奇偶（这不比判断n%2 === 0骚多了？）

console.log(5 & 1) //1
console.log(10 & 1) //0

2.用`>>` `<<` `|` `>>>`进行取整

由于JS位运算比较骚，明明浮点数内存使用64位去做存储，但是在位运算的时候，JS把数据拿出来，然后强行转成有符号的32位int类型（1位符号位，31位数字位），所以小数点在做位运算的时候，返回的还是32位的有符号整数。

console.log(1.23333 | 0) // 1
//负数也可以
console.log(-1.23 | 0) //-1
---
console.log(2.23333 << 0) //2
//负数也可以
console.log(-2.233 << 0) // -2
---
console.log(3.23333 >> 0) //3
//负数也可以
console.log(-3.2333 >> 0) //-3
---
//不可用于负数
console.log(4.23333 >>> 0) //4

3、使用`&, >>, |`来完成rgb值和16进制颜色值之间的转换

/**
  - 16进制颜色值转RGB
  - @param  {String} hex 16进制颜色字符串
  - @return {String}     RGB颜色字符串
  */
    function hexToRGB(hex) {
      var hexx = hex.replace('#', '0x')
      var r = hexx >> 16
      var g = hexx >> 8 & 0xff
      var b = hexx & 0xff
      return `rgb(${r}, ${g}, ${b})`
    }

/**
  - RGB颜色转16进制颜色
  - @param  {String} rgb RGB进制颜色字符串
  - @return {String}     16进制颜色字符串
  */
function RGBToHex(rgb) {
  var rgbArr = rgb.split(/[^\d]+/)
  var color = rgbArr[1]<<16 | rgbArr[2]<<8 | rgbArr[3]
  return '#'+ color.toString(16)
}

// -------------------------------------------------

hexToRGB('#ffffff')               // 'rgb(255,255,255)'

RGBToHex('rgb(255,255,255)')      // '#ffffff'

知识点！！

JS的最大安全整数为什么是53位
浮点数怎么转二进制
计算机怎么存储浮点数

先解决一个问题，浮点数怎么转二进制？

很简单~

//比如8.625转二进制
//先把整数部分和小数部分分开，分别转二进制
//整数部分：
parseInt(8).toString(2) // 1000
//小数部分：
//用小数不断*2，直至为1.0，每乘一次2，将整数位取走，作为二进制位的值 
0.625 * 2 = 1.25   //1，然后将整数位取走
0.25 * 2 = 0.5     //0
0.5 * 2 = 1        //1
//所以小数部分的二进制是 0.101
//再把整数和小数拼起来,就是结果  1000.101
//也可以用JSAPI验证一下
console.log(parseFloat(8.625).toString(2)) //1000.101
莫得问题~

但是计算机存储数据肯定不会存储小数点的呀，毕竟计算机底层只有0和1

那计算机怎么储存浮点数咧？

虽然JavaScript不是强类型语言，所以对于Number类型不会严格区分整型数，浮点数等，但是在JavaScript内部，数值都是以64位浮点数的形式储存

根据国际标准IEEE 754，任意一个二进制浮点数V可以表示成下面的形式：

（1）(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。 （2）M表示有效数字，大于等于1，小于2。 （3）2^E表示指数位。

举例来说：

十进制的5.0，写成二进制是101.0，相当于1.01×2^2。那么，按照上面V的格式，可以得出s=0，M=1.01，E=2。

十进制的 -5.0，写成二进制是 -101.0，相当于 -1.01×2^2。那么，按照上面V的格式，可以得出s=1，M=1.01，E=2。

IEEE 754规定，对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

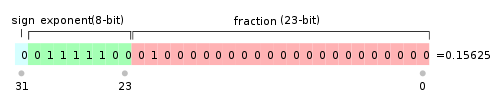
对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

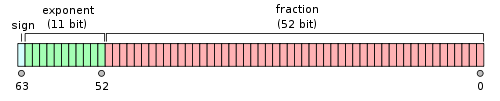
IEEE 754对有效数字M和指数E，还有一些特别规定。

前面说过，1≤M<2，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以64位浮点数为例，留给M只有52位，将第一位的1舍去以后，等于可以保存53位有效数字

（这就解答了为什么JS的最大安全整数为什么是53位，因为JS的数值是用64位数字进行存储，但是有1位是符号位，11位是指数位，只剩53位存储数字）

至于指数E，情况就比较复杂。

首先，E为一个无符号整数（unsigned int）。这意味着，如果E为8位，它的取值范围为0~~255；如果E为11位，它的取值范围为0~~2047。但是，我们知道，科学计数法中的E是可以出现负数的，*所以IEEE 754规定，***E的真实值必须再减去一个中间数***，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。*

比如，2^10的E是10，所以保存成64位浮点数时，必须保存成10+1023=1033，即10000001001

然后，指数E还可以再分成三种情况：

E不全为0或不全为1。这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。
E全为0。这时，浮点数的指数E等于1-127（或者1-1023），有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
E全为1。这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

既然公式都有了，那计算机存储浮点数只需要存储这三个变量即可

浮点数计算机存储 = 存储s + E + M的二进制

 const a = 2.25
 //a转二进制
 parseFloat(a).toString(2)
 //10.01-> (-1)^0*1.001*2^1
 //套公式
 s = 0
 E = 1024
 M = 1.001
 //答案：0+10000000000+001+`(50个0)`

小结

这下我们知道JavaScript是用64位存储数字，内部除去1位符号位，11位指数为，应该还有52位用来存储有效数字，话是这么说没错，但事实上，位操作符并不是这么认为的

。在 ECMAScript® Language Specification 中是这样描述位操作符的：

The production A : A @ B, where @ is one of the bitwise operators in the productions above, is evaluated as follows:

Let lref be the result of evaluating A.
Let lval be GetValue(lref).
Let rref be the result of evaluating B.
Let rval be GetValue(rref).
Let lnum be ToInt32(lval).
Let rnum be ToInt32(rval).
Return the result of applying the bitwise operator @ to lnum and rnum. The result is a signed 32 bit integer.

需要注意的是第5和第6步，按照ES标准，两个需要运算的值会被先转为有符号的32位整型（划重点！！！！！先被转成有符号的int类型）。所以超过32位的整数会被截断，而小数部分则会被直接舍弃。

ECMAScript 整数有两种类型，即有符号整数（允许用正数和负数）和无符号整数（只允许用正数）。在 ECMAScript 中，所有整数字面量默认都是有符号整数，这意味着什么呢？

有符号整数使用 31 位表示整数的数值，用第 32 位表示整数的符号，0 表示正数，1 表示负数。数值范围从 -2147483648 到 2147483647。

这些也就能解释上面的诡异情况啦~

前情提要

诡异情况

情况1

情况2

学习时间到

1、按位与（AND）&

2、按位或（OR）|

3、按位异或（XOR） ^

4、按位非（NOT）~

5、左移<<

6、右移>>